La prima legge di Gay-lussac

inserita il 28-01-2023

“ La prima legge di Gay-lussac è una delle tre leggi dei gas perfetti „

In questa videolezione studiamo la della prima legge di Gay-lussac o legge isobara

MATERIA: Fisica/Chimica;

Calibrato per: classi prime superiori - biennio scienze integrate

ARGOMENTO: Le leggi dei gas

La prima legge di Gay-lussac è una delle tre leggi dei gas perfetti. Sono leggi sperimentali e si basano sulla misurazione in laboratorio.

Le tre leggi dei gas perfetti analizzano il comportamento dei gas misurando le variazioni dei 3 parametri fondamentali: Temperatura, Pressione e Volume.

“ Legge di Charles o prima legge di Gay-Lussac „

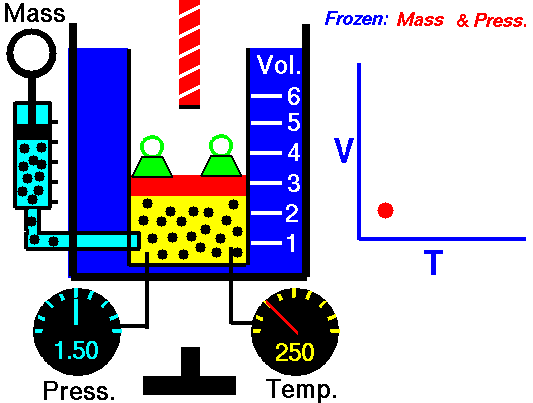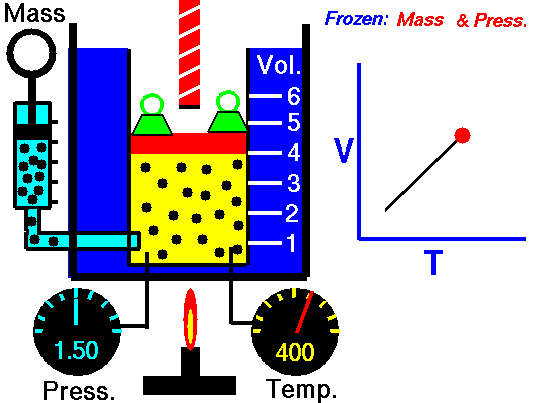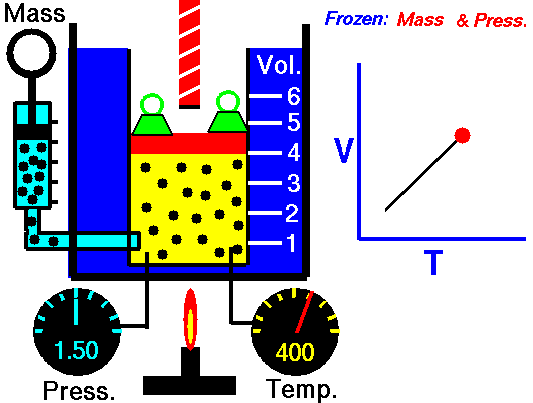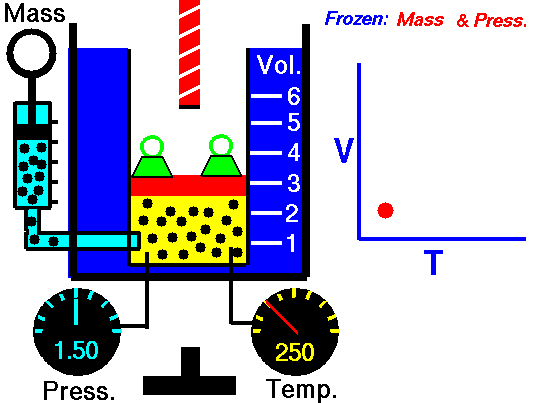
La prima legge di Gay-lussac nello specifico analizza la variazione di Volume in base alla variazione della Temperatura quando viene mantenuta la Pressione costante!; quindi la Pressione non varia in questi problemi.

Un sistema sperimentale per misurare la variazione di volume a Pressione costante può essere un cilindro graduato mobile in equilibrio con la pressione atmosferica, che può essere incrementata aggiungendo dei pesi sul coperchio del cilindro.
La pressione del gas è in equilibrio con la pressione esterna e si oppone alla compressione.
Quando aumento la Temperatura del gas il sistema raggiunge in breve tempo un nuovo equilibrio con la pressione esterna dopo aver effettuato un'espansione e raggiunto un nuovo volume superiore al precedente.

La formulazione della legge

“ Cosa afferma la prima legge di Gay-Lussac? „

La prima legge di Gay-Lussac (1802) o più propriamente legge di Charles (1787) afferma che se la pressione è costante, legge isobara (iso-stessa, bar-pressione), il volume di un gas ideale aumenta linearmente al crescere della Temperatura espressa in gradi centigradi.
L'incremento è costante e corrisponde a 1/273,15 del volume occupato dal gas a 0°C per ogni grado di temperatura.
(Questo fattore viene indicato con la lettera greca alfa α) Se invece si abbassa la temperatura sotto lo 0°C il volume decresce dello stesso valore per ogni grado di temperatura.
Possiamo esprimere matematicamente i risultati delle osservazioni sperimentali:
V_t= V₀αt  +  V₀
Dove:
V₀ = volume occupato dal gas a zero gradi centigradi
V_t = volume occupato dal gas alla temperatura t in gradi centigradi
t= temperatura a cui ho portato il gas espressa in gradi centigradi
α 1/273,15
Per cui il fattore V₀αt mi misura l'incremento del volume, da sommare a V₀, che invece è una costante se operiamo alla stessa pressione e con la stessa quantità di gas, per ottenere il volume finale raggiunto dal gas alla temperatura t

NB: se un gas è ideale una mole di gas occupa sempre un volume di 22,414 litri, alla pressione di 1 atmosfera e alla temperatura di 0°C. Molti gas reali non si discostano significativamente da questo valore.

Un problema con la temperatura in scala Celsius

Facciamo un esempio:
Un certo gas che a 0 °C occupa il volume di 170,0 litri, viene riscaldato a 80 °C, mantenendo costante la pressione. Calcola il volume del gas alla nuova temperatura.
Quindi:
V₀ = 170 Litri (l'unità di misura del volume non è un problema purché mantenuta sempre la stessa - MAI CAMBIARE LE UNITA' DI MISURA in corso d'opera! O si fa all'inizio o alla fine ma MAI tra l'inizio e la fine)
t= 80°C
α 1/273,15
V_t= volume occupato dal gas a 80°C ed è la nostra incognita!
Per cui data l'equazione:
V_t= V₀αt  +  V₀ Sostituisco:
V_t = 170 X 1/273,15 X 80 + 170 --> 49,79 + 170 --> 219,79 L
Quindi, anche se l'incremento per ogni grado sembra minimo, in realtà se la Temperatura si alza di parecchi gradi il volume aumenta in modo considerevole!!!

Prova tu:
Lo stesso gas che a 0 °C occupa il volume di 170,0 litri, viene riscaldato a 60 °C, mantenendo costante la pressione. Calcola il volume del gas alla nuova temperatura.

L'andamento della curva

Se si ripetono le misurazioni a più temperature e si riportano i dati in un grafico mettendo in ascissa la temperatura e in ordinata il volume si ottiene una retta.
Infatti se:
V_t = Y (in quanto varia in funzione di t)
t= X (la grandezza che io vario)
V₀α = m (il valore è costante per quella quantità di gas a quella pressione)
V₀ = q (il valore è costante per quella quantità di gas a quella pressione)
ottengo:
V_t =  V₀α  t  +  V₀
Y =    m  X  +  q

L'inclinazione della retta sarà data da V₀α
L'intersezione con l'asse Y sarà data dal valore di V₀ in quanto è il valore che per settaggio il volume assume alla temperatura di 0°C

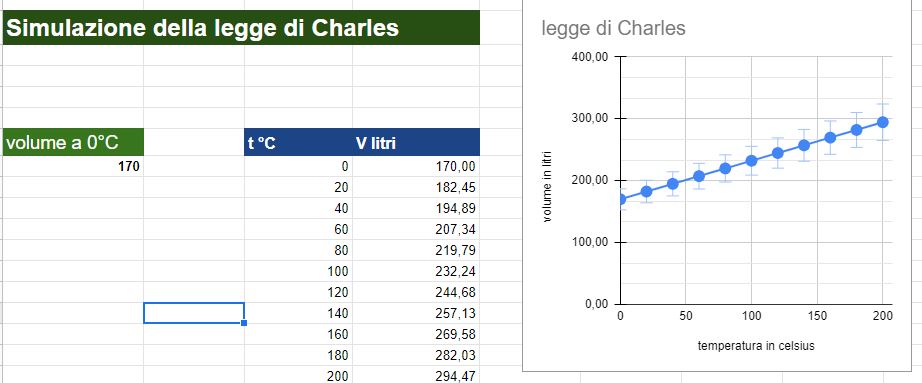
Ho inserito messo in grafico i dati di questo problema e ho analizzato la variazione del volume fino a 200 °C
Il grafico risultante è nella figura sotto. (c'è anche la soluzione al problema precedente)

Il problema del V₀

Mettiamo che ci venga dato invece un problema di questo tipo

Un certo gas che a 30 °C occupa il volume di 200,0 litri, viene riscaldato a 80 °C, mantenendo costante la pressione. Calcola il volume del gas alla nuova temperatura.

In questo caso non potremmo risolverlo con l'equazione originale in quanto non conosciamo il valore del volume del gas a 0 °C V₀
In effetti spesso e volentieri i problemi sono di questo tipo.

Per risolvere questi problemi dobbiamo operare alcuni passaggi matematici che ci permettono di svincolarci dal valore sperimentale di V₀

Vediamo come formulare la legge di Charles per semplificare la relazione sperimentale illustrata in precedenza.

V_t= V₀αt + V₀
estraiamo V₀
V_t= V₀ (1+ αt)
estraiamo α
V_t= V₀ α (1/α+ t)
se sostituiamo ad α il suo valore numerico di 1/273,15, 1 fratto 1/273,15 mi diventa semplicemente 273,15
V_t= V₀ α (273,15+ t)
Ora se invece di utilizzare i gradi centigradi usiamo i Kelvin, la cosa è molto più semplice. Infatti per passare dalla scala centigrada alla scala Kelvin basta aggiungere proprio 273,15!!!
quindi 273,15 + t è proprio il valore della temperatura in Kelvin che si indica con la T maiuscola proprio per differenziarlo dal valore in centigradi che si indica con la t minuscola.
Per cui il risultato è:
V_T= V₀α T
Ma dato che il valore di V₀α per una data quantità di uno specifico gas è costante, non varia anche se opero a piacimento a diverse temperature.
Ne consegue che: V= kT
e quindi:
V/T= k
per cui se considero due stati diversi e indico V1 il volume del gas alla temperatura T1 e V2 il volume del gas a una temperatura T2 il loro rapporto non varia. Quindi otteniamo una formulazione della legge di Charles o prima legge di Gay-Lussac più maneggevole e svincolata dalla conoscenza del valore di V₀
V1/T1=V2/T2=k

Utilizzare il simulatore del comportamento dei gas perfetti di PHET per spiegare la legge di Charles

Ho utilizzato il simulatore del comportamento dei gas perfetti presente sul sito Phet, come avevo fatto per la legge di Boyle in questa pagina, per descrivere e spiegare la prima legge di Gay-Lussac.
Per quanto riguarda la formulazione matematica ho usato direttamente quella che utilizza i gradi Kelvin in modo da poter utilizzare la relazione più semplice appena descritta.
Il grafico ottenuto con i parametri impostati nel video lo trovate alla fine della pagina
Nella prossima lezione invece vedremo come risolvere un problema sulla legge di Charles, utilizzando la Jamboard di Google per illustrare i passaggi da effetturare.

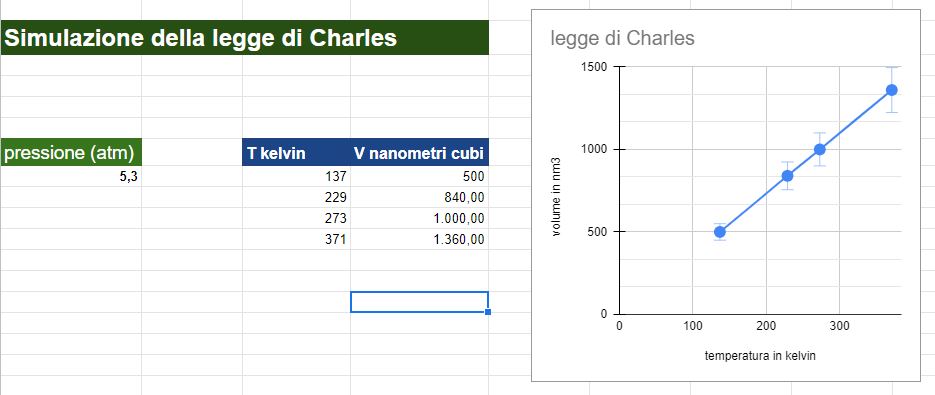
Risultati della simulazione

Nel video ho fissato 3 valori di temperatura e ho ricavato 3 valori per il volume risultante.
La pressione durante l'esperimento simulato è bloccata a 5,3 atmosfere.
Numero di particelle di gas inserite 50
Ho poi creato un file excel e graficato i risultati.
NB: la simulazione ha la limitazione che ovviamente non si possono settare volumi troppo piccoli per cui la retta risultante dai dati non può avvicinarsi all'origine del grafico. Tecnicamente allo zero assoluto, 0 Kelvin o -273,15 °C la retta raggiungerebbe l'origine e quindi un volume uguale a 0, situazione non raggungibile nella realtà.