La seconda legge di Gay-lussac

inserita il 31-01-2023

“ La seconda legge di Gay-lussac è una delle tre leggi dei gas perfetti „

In questa videolezione studiamo la seconda legge di Gay-lussac o legge isocora

MATERIA: Fisica/Chimica;

Calibrato per: classi prime superiori - biennio scienze integrate

ARGOMENTO: Le leggi dei gas

La prima legge di Gay-lussac è una delle tre leggi dei gas perfetti. Sono leggi sperimentali e si basano sulla misurazione in laboratorio.

Le tre leggi dei gas perfetti analizzano il comportamento dei gas misurando le variazioni dei 3 parametri fondamentali: Temperatura, Pressione e Volume.

“ La seconda legge di Gay-Lussac „

La seconda legge di Gay-lussac nello specifico analizza la variazione della pressione in relazione alla variazione della Temperatura quando viene mantenuto il Volume costante!; quindi il volume non varia in questi casi (iso - isos -stesso; Coro, χωροσ spazio-volume)

Analizziamola analogamente a come abbiamo fatto per la legge di Charles o prima legge di Gay-Lussac in quanto il comportamento della pressione in relazione all'andamento della temperatura è del tutto analogo a quello del volume della prima legge

Un sistema sperimentale per misurare la variazione della pressione è molto semplice: un contenitore chiuso per il gas, un fornello per scaldare e aumentare la temperatura, un contenitore con il ghiaccio per misurare la pressione a 0°C e due sensori per misurare la Temperatura e la pressione all'interno del contenitore, o un termometro e un manometro.

La formulazione della legge

“ Cosa afferma la seconda legge di Gay-Lussac? „

La seconda legge di Gay-Lussac (1802) afferma che se il volume è costante, legge isocora, la pressione di un gas ideale aumenta linearmente al crescere della Temperatura espressa in gradi centigradi.
L'incremento è costante e corrisponde a 1/273,15 della pressione esercitata dal gas a 0°C per ogni grado di temperatura.
(Questo fattore viene indicato con la lettera greca alfa α) Se invece si abbassa la temperatura sotto lo 0°C il volume decresce dello stesso valore per ogni grado di temperatura.
Possiamo esprimere matematicamente i risultati delle osservazioni sperimentali:
P_t= P₀αt  +  P₀
oppure P_t= P₀ (1  + αt)
Dove:
P₀ = pressione esercitata dal gas a zero gradi centigradi
P_t = pressione esercitata dal gas alla temperatura t in gradi centigradi
t= temperatura a cui ho portato il gas espressa in gradi centigradi
α 1/273,15
Per cui il fattore P₀αt mi misura l'incremento della pressione, da sommare a P₀, che invece è una costante se operiamo con lo stesso volume di partenza e la stessa quantità di gas, per ottenere la pressione finale raggiunta dal gas alla temperatura t

Perché la pressione aumenta all'aumentare della temperatura e diminuisce al diminuire della temperatura?

Bisogna considerare che la pressione che un gas esercita sulle pareti del recipiente dipende dal numero degli urti delle particelle nell'unità di tempo e dall'energia cinetica di questi urti che è associata alla velocità delle particelle.
Dato che il volume del recipiente è fisso e non vario la quantità di gas e quindi il numero delle particelle, entrambi i fattori dipenderanno solo dalla Temperatura!
Infatti ricordiamo che la temperatura è una misura dell'energia cinetica media delle particelle di un corpo. A un aumento della Temperatura corrisponde un aumento della velocità delle particelle e dell'energia cinetica associata a tale movimento.
Un aumento drammatico della temperatura può conferire alla particelle una quantità di energia cinetica tale, e un valore di pressione tale da rompere il recipiente.

Un problema con la temperatura in scala Celsius

Facciamo un esempio:
8 litri di un gas a 0 °C esercitano una pressione di 4 atmosfere.
Che pressione eserciterà il gas se la temperatura viene portata a 100 °C?
Quindi:
P₀ = 4 atmosfere (atm) (l'unità di misura della pressione non è un problema purché mantenuta sempre la stessa - MAI CAMBIARE LE UNITA' DI MISURA in corso d'opera! O si fa all'inizio o alla fine ma MAI tra l'inizio e la fine)
Un convertitore di pressione lo trovate a questa pagina del sito.
t= 100°C
α 1/273,15
P_t= pressione esercitata dal gas a 100°C ed è la nostra incognita!
Per cui data l'equazione:
P_t= P₀αt  +  P₀ Sostituisco:
P_t = (4 atm X 1/273,15 X 100) + 4 atm --> 1,46 atm + 4 atm -->5,46 atm

Un problema con la temperatura in scala Celsius con la temperatura come incognita

Visto che non l'abbiamo fatto nella pagina sulla Legge di Charles, risolviamo qui un problema un po' meno lineare in cui l'incognita non sia la pressione ma la temperatura dopo il riscaldamento.

Facciamo un esempio:
8 litri di un gas si trovano a 0 °C ed esercitano una pressione di 4 atmosfere. (lo stesso di prima)
A che temperatura dovrò portare il gas affinché la sua pressione sia di 9 atmosfere?
Quindi:
P₀ = 4 atmosfere (atm)
t= ? - è la mia incognita
α 1/273,15
P_t= 9 atmosfere
Ora, il modo più semplice di risolvere questo tipo di problemi è quello di usare la temperatura assoluta e la proporzionalità diretta come vediamo nel video.
Però proviamo a risolverlo usando la formula empirica appena descritta.
P_t= P₀αt  +  P₀
da cui
P_t= P₀ (1  + αt)
portiamo P₀dall'altro lato dell'equazione (va al denominatore)
P_t/P₀ = 1  + αt
Portiamo anche 1 dall'altra parte
P_t/P₀ - 1 =  αt
cioè
9/4 - 1 =  αt --> 1,25 =  αt
dato che α è 1/273,15, se la porto dall'altro lato mi si "ribalta" e diventa 273,15
per cui
1,25 X 273,15 =  t
quindi
t =  341,44 °C
Per cui per portare la pressione da 4 a 9 atmosfere bisogna portare la temperatura da 0 °C a 341,44 °C

Prova tu:
Lo stesso gas che a 0 °C esercita una pressione di 4 atm, viene riscaldato fino a raddoppiare la pressione; qual è la temperatura raggiunta dal gas?

L'andamento della curva (analogo alla legge di Charles)

Se si ripetono le misurazioni a più temperature e si riportano i dati in un grafico mettendo in ascissa la temperatura e in ordinata la pressione si ottiene una retta.
Infatti se:
P_t = Y (in quanto varia in funzione di t)
t= X (la grandezza che io vario)
P₀α = m (il valore è costante per quella quantità di gas a quella pressione)
P₀ = q (il valore è costante per quella quantità di gas a quella pressione)
ottengo:
P_t =  P₀α  t  +  P₀
Y =    m  X  +  q

L'inclinazione della retta sarà data da P₀α
L'intersezione con l'asse Y sarà data dal valore di P₀ in quanto è il valore che per settaggio il volume assume alla temperatura di 0°C

L'intersezione con l'asse X

Dato che questi aspetti li abbiamo già trattati nella pagina della legge di Charles aggiungiamo qualcosa.
Abbiamo visto che l'intersezione con l'asse Y si ha nel punto P₀
Ma in quale punto si ha l'intersezione con l'asse X? (l'asse della temperatura?)

L'intersezione con l'asse X si ha virtualmente quando il valore di P_t è zero.
da cui
P_t= P₀ (1  + αt)
0 =  P₀ (1  + αt)
dato che P₀ è ≠ da 0 (è 4 atmosfere) allora il valore tra parentesi (1  + αt) deve essere uguale a zero per soddisfare l'equazione
quindi
(1  + αt)  =   0
porto 1 dall'altro lato
αt =   -1
porto α dall'altro lato (sempre 1/273,15 si "ribalta" e diventa 273,15)
quindi moltiplichiamo 273,15 x -1
t =   -273,15 °C
che corrisponde allo ZERO ASSOLUTO cioè lo Zero della scala Kelvin

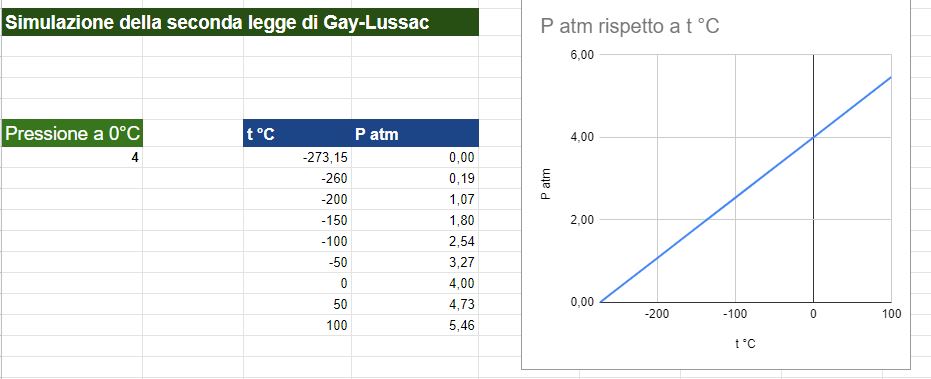
Ho inserito messo in grafico i dati di questo problema fino a -273,15 °C
Il grafico risultante è nella figura sotto.

Il problema del P₀ analogo alla legge di Charles

Come per la legge di Charles possiamo formulare la seconda legge di Gay-Lussac con la temperatura assoluta in modo da svincolarci dal valore P₀ e ottenere una equazione risolutiva più semplice.

P_t= P₀αt + P₀
estraiamo P₀
P_t= P₀ (1+ αt)
estraiamo α
P_t= P₀α (1/α+ t)
se sostituiamo ad α il suo valore numerico di 1/273,15, 1 fratto 1/273,15 mi diventa semplicemente 273,15
P_t= P₀α (273,15+ t)
Ora se invece di utilizzare i gradi centigradi usiamo i Kelvin, la cosa è molto più semplice. Infatti per passare dalla scala centigrada alla scala Kelvin basta aggiungere proprio 273,15!!!
quindi 273,15 + t è proprio il valore della temperatura in Kelvin che si indica con la T maiuscola proprio per differenziarlo dal valore in centigradi che si indica con la t minuscola.
Per cui il risultato è:
P_T= P₀α T
Ma dato che il valore di P₀α per una data quantità di uno specifico gas è costante, non varia anche se opero a piacimento a diverse temperature.
Ne consegue che: P= kT
e quindi:
P/T= k
per cui se considero due stati diversi e indico V1 il volume del gas alla temperatura T1 e V2 il volume del gas a una temperatura T2 il loro rapporto non varia. Quindi otteniamo una formulazione della legge di Charles o prima legge di Gay-Lussac più maneggevole e svincolata dalla conoscenza del valore di V₀
P1/T1=P2/T2=k

Utilizzare il simulatore del comportamento dei gas perfetti di PHET per spiegare la seconda legge di Gay-Lussac

Ho utilizzato il simulatore del comportamento dei gas perfetti presente sul sito Phet, come avevo fatto per la legge di Boyle e la prima legge di Gay-Lussac.
Per quanto riguarda la formulazione matematica ho usato direttamente quella che utilizza i gradi Kelvin in modo da poter utilizzare la relazione più semplice appena descritta.
Il grafico ottenuto con i parametri impostati nel video lo trovate alla fine della pagina
Nella prossima lezione invece vedremo come risolvere un problema sulla seconda legge di Gay-Lussac, in Kelvin, utilizzando la Jamboard di Google per illustrare i passaggi da effetturare.

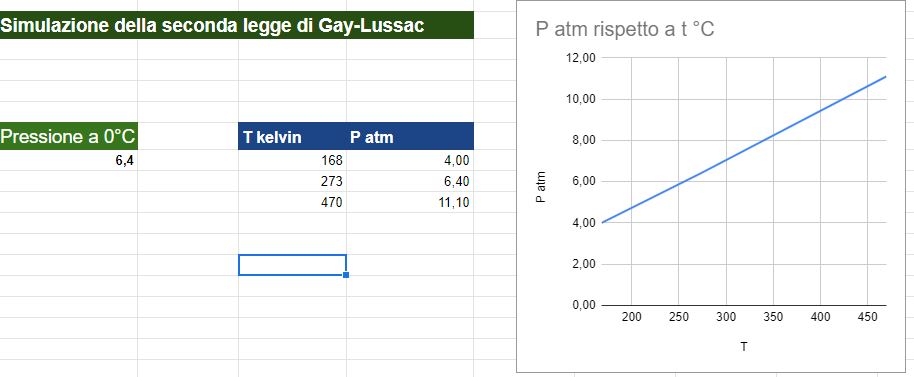
Risultati della simulazione

Nel video ho fissato 3 valori di temperatura e ho ricavato 3 valori per il volume risultante.
Il volume del recipiente del simulatore è bloccato a 830 nm³
Numero di particelle di gas inserite 50
Ho poi creato un file excel e graficato i risultati.
NB: Come nel caso della legge di Charles non posso scendere troppo con la temperatura per cui la retta risultante dai dati non si avvicina allo zero assoluto. Tecnicamente allo zero assoluto, 0 Kelvin o -273,15 °C la retta raggiungerebbe l'origine e quindi, come abbiamo detto sopra, la pressione avrebbe un valore di 0, situazione non raggungibile nella realtà.